調(diào)節(jié)閥作為流量控制系統(tǒng)中的重要元件，通過改變其自身阻力特性調(diào)節(jié)系統(tǒng)的介質(zhì)流量，其調(diào)節(jié)質(zhì)量影響到整個(gè)系統(tǒng)的效率和穩(wěn)定性。依照系統(tǒng)的調(diào)節(jié)需要設(shè)計(jì)調(diào)節(jié)閥，關(guān)鍵是設(shè)計(jì)調(diào)節(jié)閥結(jié)構(gòu)及其閥芯的流通面積分布。

目前已有的關(guān)于調(diào)節(jié)閥流量特性的研究主要集中在以下幾個(gè)方面，一是流量調(diào)節(jié)理論的研究，包括數(shù)學(xué)模型的建立和完善、評價(jià)標(biāo)準(zhǔn)的討論等。二是針對具體閥型，利用試驗(yàn)或工程經(jīng)驗(yàn)，分析流量特性和改進(jìn)方法；三是針對具體閥型，利用CED技術(shù)分析流量特性-。。對于流量特性與流通面積分布兩者之間聯(lián)系的討論，文獻(xiàn)中闡述了借助實(shí)驗(yàn)數(shù)據(jù)和流體阻力系數(shù)一流通面積間線圖，或利用總流量系數(shù)等參數(shù)，計(jì)算特定形式調(diào)節(jié)閥的流通面積分布的方法；文獻(xiàn)[ 8」中也針對具體調(diào)節(jié)閥，提出了通過調(diào)整面積一行程分布改善流量特性的方案，并與實(shí)驗(yàn)結(jié)果進(jìn)行了比較。然而這些研究都是針對具體形式的調(diào)節(jié)閥，且依賴經(jīng)驗(yàn)數(shù)據(jù)和實(shí)驗(yàn)數(shù)據(jù)，其意義在于具體工程應(yīng)用，并沒有在理論層面分析流量特性與流通面積分布之間的聯(lián)系。而網(wǎng)孔型套筒閥的流量特性，也沒有相關(guān)文獻(xiàn)對其進(jìn)行分析。

本文設(shè)計(jì)了兩種不同結(jié)構(gòu)的簡化模型，對其進(jìn)行數(shù)值模擬研究，旨在分析其流量特性與流通面積分布關(guān)系之間的聯(lián)系，從中尋找規(guī)律。在此基礎(chǔ)上，對一種網(wǎng)孔型套筒閥進(jìn)行了優(yōu)化，計(jì)算了優(yōu)化前后兩種調(diào)節(jié)閥的流量特性，并進(jìn)行了比較分析。

調(diào)節(jié)閥的流量特性

調(diào)節(jié)閥的流量特性是指通過調(diào)節(jié)閥的流體的相對流量與相對開度之間的關(guān)系，包括理想流量特性和工作流量特性。

理想流量特性

流量控制系統(tǒng)由調(diào)節(jié)閥和其他系統(tǒng)元件共同構(gòu)成，系統(tǒng)流量取決于系統(tǒng)的總阻力。因此，在不同的系統(tǒng)中，即使是相同的調(diào)節(jié)閥、相同的開度，流量也并不相同。而調(diào)節(jié)閥的理想流量特性能夠反映調(diào)節(jié)閥自身的調(diào)節(jié)特性：即調(diào)節(jié)閥前后壓差恒定的情況下，相對流量與相對開度之間的關(guān)系為調(diào)節(jié)閥理想流量特性（也稱調(diào)節(jié)閥的固有特性），其關(guān)系曲線稱為理想流量特性曲線，用數(shù)學(xué)表達(dá)式（l)表示。

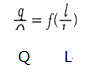
式中：q/Q為相對流量；//L為相對開度。

在常見的調(diào)節(jié)閥中，有四種典型的流量特性曲線，即直線型、對數(shù)型（也稱等百分比型）、快開型、拋物線型」，分別對應(yīng)圖1中的曲線1、2、3、4。直線型流量特性的調(diào)節(jié)閥，流量隨行程線性變化，在小開度時(shí)流量變化明顯（流量變化量與流量的比值大），調(diào)節(jié)靈敏度高，而在大開度時(shí)，流量變化相對緩慢（流量變化量與流量的比值小），調(diào)節(jié)靈敏度低，因而出現(xiàn)大開度下調(diào)節(jié)能力不足等問題，因此在一些情況下不能滿足調(diào)節(jié)要求。對數(shù)型流量特性的調(diào)節(jié)閥，流量變化速度逐漸加快，小開度時(shí)流量變化緩慢，調(diào)節(jié)精度高，大開度時(shí)流量變化相對較快，能保持良好的調(diào)節(jié)能力，這些特點(diǎn)使其在工程中得到了廣泛的應(yīng)用。拋物線型調(diào)節(jié)閥的調(diào)節(jié)特性介于直線型和對數(shù)型兩者之間田，這種特性的調(diào)節(jié)閥在工程應(yīng)用中也比較常見。快開型調(diào)節(jié)閥的調(diào)節(jié)特點(diǎn)與對數(shù)型相反，小開度時(shí)流量迅速變化，達(dá)到快速加大流量的目的，而大開度時(shí)流量變化緩慢。除了這四種典型曲線外，還有雙曲線型、平方根型等流量特性曲線，但并不常見。

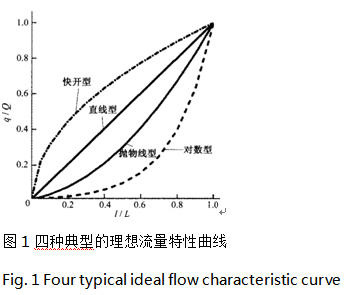
事實(shí)上，具體到實(shí)際的調(diào)節(jié)閥時(shí)，其理想流量特性曲線很難與四種典型的理想流量特性曲線完全重合，往往是近似某種形式，如普通蝶閥的理想流量特性通常介于直線型和對數(shù)型曲線之間。選擇和設(shè)計(jì)調(diào)節(jié)閥時(shí)，須根據(jù)具體要求選擇適當(dāng)?shù)牧髁刻匦郧€作為設(shè)計(jì)參考。

對于某些結(jié)構(gòu)形式的調(diào)節(jié)閥，根據(jù)經(jīng)驗(yàn)公式或?qū)嶒?yàn)參數(shù)，可以得到其理想流量特性曲線與流通面積分布之間的關(guān)系，據(jù)此可以由選定的理想流量特性曲線計(jì)算調(diào)節(jié)閥的流通面積分布。針對幾種具體結(jié)構(gòu)形式的調(diào)節(jié)閥，文獻(xiàn)[ 0中介紹了計(jì)算流通面積分布的方法，但都需要實(shí)驗(yàn)或經(jīng)驗(yàn)參數(shù)作為條件，并不適用于其他結(jié)構(gòu)的調(diào)節(jié)閥。

工作流量特性

安裝在調(diào)節(jié)系統(tǒng)中的調(diào)節(jié)閥，隨著管路阻力等工作條件的變化，調(diào)節(jié)閥的前后壓差不再保持恒定，此時(shí)調(diào)節(jié)閥的相對流量與相對行程之間的關(guān)系稱為調(diào)節(jié)閥的工作流量特性。用數(shù)學(xué)表達(dá)式表示為：

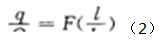
Q L 式中符號意義同公式（1)。 理想流量特性曲線和工作流量特性曲線可以通過公式（3）建立聯(lián)系「2」。

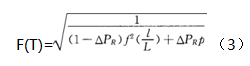
式中PR為壓降比，表示調(diào)節(jié)閥前后壓差占調(diào)節(jié)系統(tǒng)總壓降的比值。

文獻(xiàn)[ 7 ]中闡述了選取壓降比APR的方法，若壓降比選定，則可依照公式（3）岫系統(tǒng)需求的工作流量特性曲線推導(dǎo)出對應(yīng)的理想流量特性曲線，若理想流量特性曲線與流通面積分布的關(guān)系已知，便可推求調(diào)節(jié)閥的流通面積分布。

簡化模型的流量特性分析

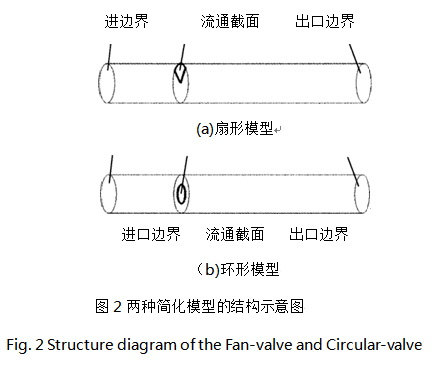
本文設(shè)計(jì)了兩種調(diào)節(jié)閥的簡化模型，根據(jù)其流通截面的形狀，分別稱之為扇形模型和環(huán)形模型，其流通截面的結(jié)構(gòu)如圖2 所示。扇形模型的流通截面為扇形，設(shè)定其在0、360。范圍內(nèi)隨行程均勻變化，流通面積與行程的關(guān)系為線性。環(huán)形模型的流通截面為圓形，設(shè)定其直徑隨行程均勻變化，易知其流通面積與行程的關(guān)系為平方關(guān)系。需要說明的是，此兩種模型并不能直接適用工程應(yīng)用，本文用來計(jì)算，旨在理論研究。

數(shù)值計(jì)算

本文的數(shù)值模擬研究基于PROE軟件建模,GAMBIT軟件劃分網(wǎng)格、FLUENT軟件求解。按圖2中所示的結(jié)構(gòu)建立模型：管路直徑] 200 mm，管道長度取閥前2，100 mm,閥后 20 000 mm（初步計(jì)算取5倍直徑時(shí)出口有回流），分別建立調(diào)節(jié)閥在不同開度下的模型。網(wǎng)格劃分：采用非結(jié)構(gòu)網(wǎng)格劃分，扇形模型總網(wǎng)格數(shù)量為13萬個(gè)左右，環(huán)形模型為10萬個(gè)左右，扇形模型垂直于軸向的橫截面上網(wǎng)格形狀如圖3，網(wǎng)格沿軸向均勻分布，環(huán)形模型類似。求解計(jì)算：設(shè)置定常流動，選用標(biāo)準(zhǔn)湍流模型，設(shè)置流體介質(zhì)為水一1 kg/L),進(jìn)出口壓差為105 Pa（進(jìn)口總壓105 Pa，出口表壓0 (a)o通過計(jì)算不同開度下的流量，擬合出模型的理想流量特性曲線，如圖4。